Законы алгебры логики
- Табличный способ определения истинности сложного выражения имеет ограниченное применение, так как при увеличении числа логических переменных приходится перебирать слишком много вариантов. В таких случаях используют способ приведения формул к нормальной форме.
- Формула имеет нормальную форму, если в ней используются только знаки конъюнкции, дизъюнкции и отрицания, при этом знаки отрицания находятся только при переменных, и нет двойного отрицания.
- Для преобразований формул в равносильные важную роль играют равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел принято называть законами.

Порядок упрощения
Шаг 1. Заменить исключающее ИЛИ, эквивалентность и импликацию на их выражения через дизъюнкцию, конъюнкцию и инверсию.
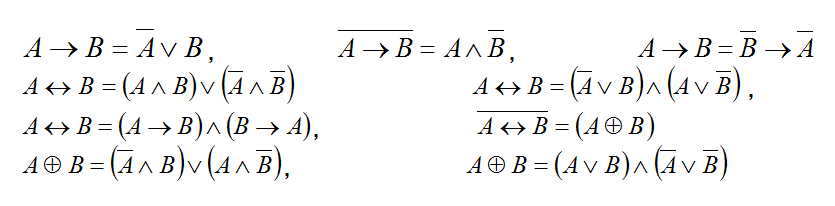
Шаг 2. Раскрыть инверсию по законам де Моргана.
Шаг 3. Применить законы алгебры логики, стараясь максимально сократить количество операций.
Пример 1. Упростить выражение:

Виды формул алгебры высказываний:
1.Выполнимая – т.е. хотя бы на одном наборе значений переменных будет ИСТИНА.
2.Опровержимая – т.е. хотя бы на одном наборе значений переменных будет ЛОЖНА.
3.Тавтология – формула, которая на любом наборе переменных будет ИСТИНА.
4.Противоречие - формула, которая на любом наборе переменных будет ЛОЖНА.
Пример 2. Составьте таблицу истинности и укажите будет ли формула выполнимой, опровержимой, тавтологией или противоречием.
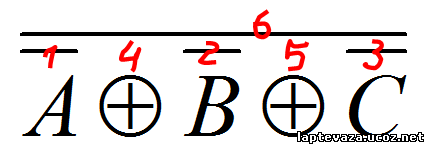
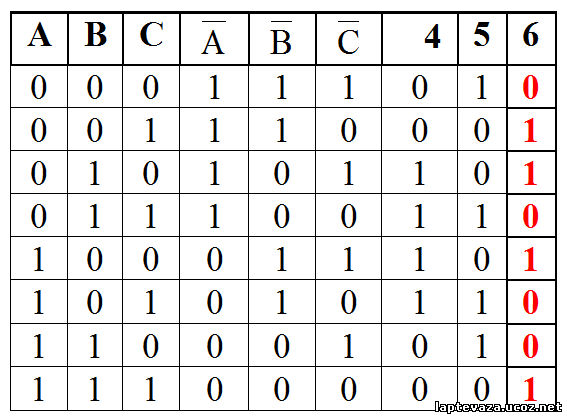
Первая формула выполнима (имеет 1), формула опровержима (имеет 0), не является ни противоречием ни тавтологией
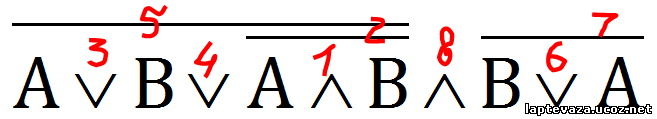
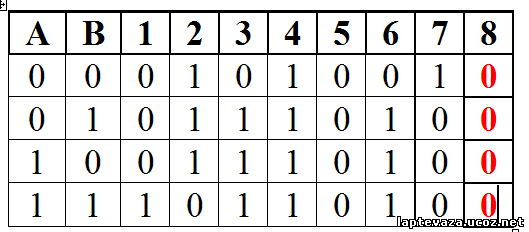
Вторая формула не выполнима (не имеет 1), опровержима (имеет 0), не является тавтологией, является противоречием.
Две формулы называются равносильными, если на любых одинаковых наборах значений пропозиционных переменных, значения формул совпадают.
Пример 3. Докажите тождество с помощью таблиц истинности.
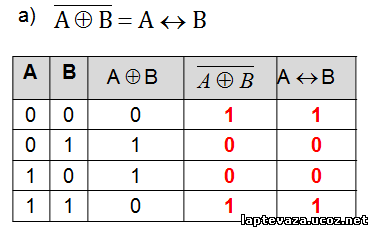
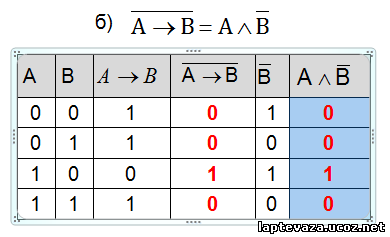
А) , б) и в первом и во втором случаях функции равносильны, т.е тождественны.




