Базовые алгоритмические конструкции
Человеку в жизни и практической деятельности приходится решать множество различных задач. Решение каждой из них описывается своим алгоритмом, и разнообразие этих алгоритмов очень велико. Вместе с тем для записи любого алгоритма достаточно трёх основных алгоритмических конструкций (структур): следования, ветвления, повторения. Это положение выдвинул и доказал Э. Дейкстра в 70-х гг. прошлого века.
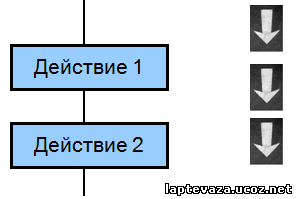
I. Следование — алгоритмическая конструкция, отображающая естественный, последовательный порядок действий. Алгоритмы, в которых используется только структура «следование», называются линейными алгоритмами. Графическое представление алгоритмической конструкции представлено на рисунке.
Пример 1. Дан фрагмент линейного алгоритма:
- х:=2
- у:=х*х
- у:=у*у
- х:=у*х
- s:=x+y
|
Шаг алгоритма |
Переменные |
||
|
1 |
x |
y |
s |
|
1 |
2 |
- |
- |
|
2 |
2 |
4 |
- |
|
3 |
2 |
16 |
- |
|
4 |
32 |
16 |
- |
|
5 |
32 |
16 |
48 |
Выясним, какое значение получит переменная s после выполнения этого фрагмента алгоритма. Для этого составим таблицу (таблица трассировки) значений переменных, задействованных в алгоритме:
Составленная нами таблица значений переменных моделирует работу исполнителя этого алгоритма.

II. Ветвление - алгоритмическая конструкция, в которой в зависимости от результата проверки условия («да» или «нет») предусмотрен выбор одной из двух последовательностей действий (ветвей).
Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.
Блок-схема ветвления представлена на рисунке. Каждая ветвь может быть разной степени сложности, а может вообще не содержать предписаний.
| Полная форма ветвления | Сокращённая форма ветвления |
| если <условие>
то <действие 1> иначе <действие 2> все |
если <условие> то <действия 1> все |
|
Пример алг правописание частиц НЕ, НИ нач если частица под ударением то писать НЕ иначе писать НИ все кон |
Пример: алг сборы на прогулку нач если на улице дождь то взять зонтик все кон |
Для записи условий, по которым разветвляется алгоритм используются операции сравнения:
А<В — А меньше В;
А<=B — А меньше или равно B;
А=В — A равно B;
А>В — А больше B;
А>=В — А больше или равно В;
А<>В — A не равно B.
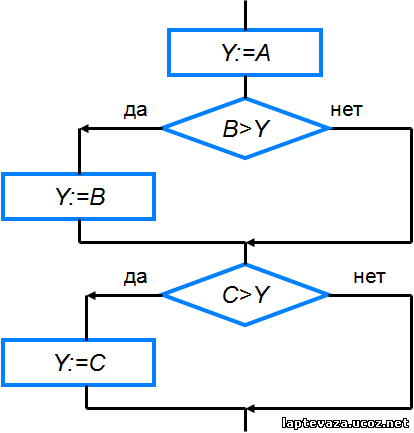
Пример 2. Переменной Y присваивается значение большей из трёх величин A, B и C.
|
Шаг |
Константы |
Переменная |
Условие |
||
|
А |
В |
С |
Y |
||
|
10 |
30 |
20 |
|||
|
1 |
|
|
|
10 |
|
|
2 |
|
|
|
|
30 > 10 (Да) |
|
3 |
|
|
|
30 |
|
|
4 |
|
|
|
|
20 > 30 (Нет) |




