Логические операции и функции

Пусть даны два произвольных высказывания А и В.

1. Выражение АΛВ означает высказывание, истинное только тогда, когда А и В истинны. Такое высказывание называется конъюнкцией высказывания А и В. В обычной речи этой операции соответствует соединение высказываний союзом «И», «А», «ДА». Будем считать, что если А, В истинны, то они соответственно принимают значение 1, ложно – 0.

Обозначения:     И, &, and,Λ ,•.

А	В	АΛВ
0	0	0
1	0	0
0	1	0
1	1	1

Пример:

А – число 36 четное

В – число 36 двузначное

АΛВ – число 36 четное и двузначное

 

2. Выражение АVВ означает высказывание, истинное, когда, по крайне мере одно из высказывание А или В истинно. Такое высказывание называется дизъюнкцией высказываний А и В. В обычной речи этой операции соответствует соединение высказыванием связкой «ИЛИ».

Обозначения: ИЛИ, OR, V, +, 

А	В	АVВ
0	0	0
1	0	1
0	1	1
1	1	1

Пример:

А - число 36 четное

В - число 36 двузначное

А V В - число 36 четное или двузначное

 

3. ИНВЕРСИЯ (логическое отрицание) делает истинное высказывание ложным, а ложное — истинным. В обычной речи этой операции соответствует образование нового высказывания с помощью частицы НЕ.

Обозначения: ¬A, Ā, not A

А	Ā
0	1
1	0

Пример:

А - число 36 четное

Ā - Неверно, что число 36 четное. Число 36 не четное

 

4. Выражение А → B  означает высказывание, которое ложно тогда и только тогда, когда А истинно, а В ложно. Такое высказывание называется импликацией высказываний А и В. Читается «А влечет В» или «если А, то В».

Обозначения:  А → B, ⇒

А	В	А → B
0	0	1
0	1	1
1	0	0
1	1	1

Пример:

А →  В – если число 36 четное, то оно  двузначное

А → В – Если 2>3, то крокодилы летают

 

5. Выражение А « B означает высказывание, которое истинно тогда и только тогда, когда А и В оба истинны, или оба ложны. Такое высказывание называется эквивалентностью. В обычной речи этой операции соответствует соединение высказывания «тогда и только тогда, когда».  

Обозначения:  

А	В	А⇔B
0	0	1
0	1	0
1	0	0
1	1	1

 

Пример:

А ⇔ В – число 36 четное тогда и только тогда, когда оно  двузначное.

А ⇔ В – чтобы число делилось на 10, необходимо и достаточно что бы оно оканчивалось нулем.

 

6. Операцией Исключающее ИЛИ  (антиэквивалентность) высказываний А, В называют составное высказывание, которое истинно тогда и только тогда, когда значение истинности высказываний А, В противоположны и ложно в противном случае, что отражается таблицей истинности.

Обозначения: 

А	В	АВ
0	0	0
0	1	1
1	0	1
1	1	0

Пример:

А  В – Либо число четное, либо двузначное

 

 

Приоритет операций — это порядок выполнения логических операций и функций в высказывании.

Приоритет логических операций:

1. Операции в скобках.
2. Инверсия (¬ А).
3. Конъюнкция (А Λ В).
4. Дизъюнкция (А V В).
5. Импликация (А → В).
6. Эквивалентность (А « В),
7. Исключающее ИЛИ (А Å В).

Таблицы истинности

Решение логических выражений принято оформлять в виде таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.        

Для составления таблицы истинности необходимо:

1. выяснить количество строк (2ⁿ, где n – количество переменных);
2. выяснить количество столбцов (количество переменных + количество логических операций);
3. построить таблицу, указывая названия столбцов и возможные наборы значений переменных;
4. заполнить таблицу истинности по столбцам.

Пример 1. Построим таблицу истинности для функции F = (АV В) Λ (¬A V ¬B)

1. Переменных: две (А и В), т.е. N = 2 ⇒ количество строк: 2ⁿ=2²=4. С заголовком: 5
2. Количество столбцов: 2 переменные + 5 операций (V,V,¬,Λ и ¬). Итого 7

Порядок операций:

A	B	(АV В)	¬A	¬B	¬A V ¬B	(АV В) Λ (¬A V ¬B)
0	0	0	1	1	1	0
0	1	1	1	0	1	1
1	0	1	0	1	1	1
1	1	1	0	0	0	0

Пример 2. Определить логическое значение формулы:

 

                                           

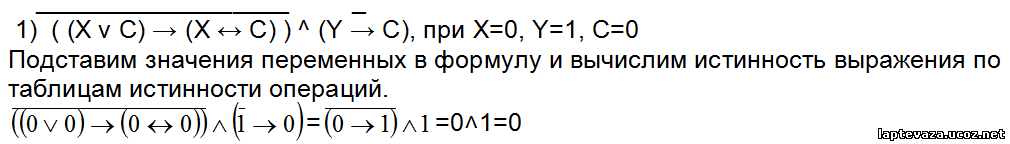
Задания к ЕГЭ по теме "Логика"