Этапы решения задач на компьютере

     Компьютерные программы программисты создают для решения разнообразных задач. Программирование — важный, но не единственный этап решения задачи на компьютере. Чтобы решать задачи на компьютере, необходимо владеть языком программирования, обладать знаниями в области информационного моделирования и алгоритмизации.

   Решение задачи с использованием компьютера включает в себя 5 этапов

   На первом этапе обычно строится словесная информационная модель объекта или процесса. При этом должно быть четко определено, что дано (какие исходные данные известны, какие данные допустимы) и что требуется найти в решаемой задаче. Также должны быть четко выделены наиболее существенные свойства рассматриваемого объекта, указаны связи между исходными данными и результатами.

   На втором этапе описательная информационная модель формализуется, т. е. записывается с помощью некоторого формального языка. Для этого требуется:

• понять, к какому классу принадлежит рассматриваемая задача;
• записать известные связи между исходными данными и результатами с помощью математических соотношений;
• выбрать наиболее подходящий способ для решения задачи.

   На третьем этапе осуществляется построение алгоритма — чёткой инструкции, задающей необходимую последовательность действий для решения задачи. Алгоритм чаще всего представляется в форме блок-схемы, ввиду её наглядности и универсальности.

   На четвёртом этапе алгоритм записывается на одном из языков программирования. Вы учитесь записывать программы на языке Паскаль.

   На пятом этапе осуществляется отладка и тестирование программы. Этап отладки и тестирования также называют компьютерным экспериментом.

   Отладка программы — это процесс проверки работоспособности программы и исправления обнаруженных при этом ошибок. Ошибки могут быть связаны с нарушением правил записи программы на конкретном языке программирования. Их программисту помогает выявить используемая система программирования; она выдаёт на экран сообщения о выявленных ошибках.

   Проверка правильности разработанной программы осуществляется с помощью тестов. Тест — это конкретный вариант значений исходных данных, для которого известен ожидаемый результат.

Рассмотрим последовательность прохождения этапов решения задачи на компьютере на примере простой задачи.

Водитель автомобиля, движущегося с некоторой постоянной скоростью, увидев красный свет светофора, нажал на тормоз. После этого скорость автомобиля стала уменьшаться каждую секунду на 5 метров. Требуется найти расстояние, которое автомобиль пройдёт до полной остановки.

Первый этап.

Дано:

v0x - начальная скорость;

vx - конечная скорость (равна нулю);

ax - ускорение (равно -5 м/с)

Требуется найти: - расстояние, которое пройдёт автомобиль до полной остановки.

Второй этап. В данной ситуации мы имеем дело с прямолинейным равноускоренным движением тела. Формула для перемещения при этом имеет вид:

 

 

 

 

 

 

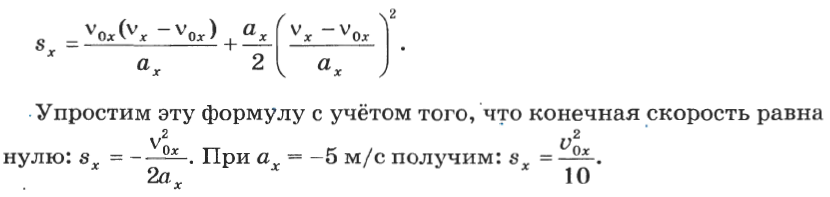
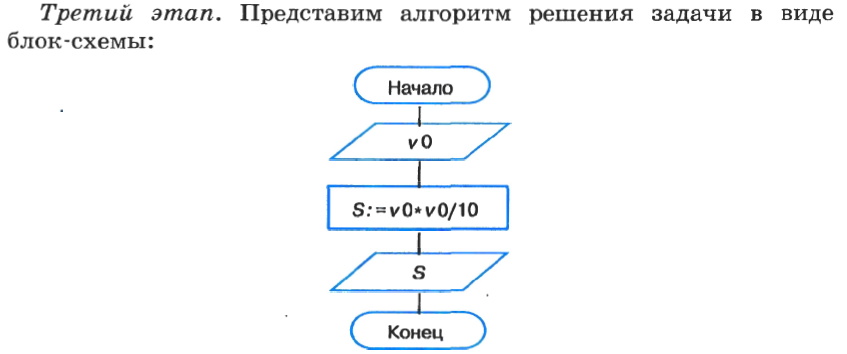
Четвёртый этап. Запишем данный алгоритм на языке программирования Паскаль:

program п_2;

var vO, s: real;

begin

writeln('Вычисление длины пути торможения автомобиля 1);

write('Введите начальную скорость (м/с)> ');

readln (vO); s:=v0*v0/10;

writeln ('До полной остановки автомобиль пройдет s : 8 : 4, 1 м. ' )

end.

     Пятый этап. Протестировать составленную программу можно, используя ту информацию, что при скорости 72 км/ч с начала торможения до полной остановки автомобиль проходит 40 метров.

     Выполнив программу несколько раз при различных исходных данных, можно сделать вывод: чем больше начальная скорость автомобиля, тем большее расстояние он пройдет с начала торможения до полной остановки.

     Применяя компьютер для решения задач, всегда следует помнить, что наряду с огромным быстродействием и абсолютной исполнительностью у компьютера отсутствуют интуиция и чувство здравого смысла, и он способен решать только ту задачу, программу решения которой ему подготовил человек.

Линейные алгоритмы

Программы, реализующие линейные алгоритмы, являются простейшими. Все имеющиеся в них операторы выполняются последовательно, один за другим.

Программируя линейные алгоритмы, рассмотрим более подробно целочисленные, логические, символьные и строковые типы данных.

1) Числовые типы данных:

Функция	Назначение	Тип аргумента	Тип результата
abs (x)	Модуль  x	integer, real	Такой же, как у аргумента
sqr (x)	Квадрат x	integer, real	Такой же, как у аргумента
sqrt (x)	Квадратный корень из x	integer, real	real
exp(x)	возвращает экспоненту от х (ех)
ln(x)	возвращает натуральный логарифм х
rouid (x)	Округление  х до ближайшего целого	real
frac (x)	Целая часть x	real
int (x)	Дробная часть x	real
sin(x)	возвращает синус х
cos(x)	возвращает косинус х
arctan(x)	возвращает арктангенс х
random	Случайное число от 0 до 1	-	real
random (x)	Случайное число от 0 до x	integer	integer

 

 

 

 

 

 

 

 

 

 

 

Исследование функций round, int и frac

program n_3;

 var x: real;

begin

  writeln ('Исследование функций round, int, frac');

  write ('Введите x>>');

  readln (x);

  writeln ('Округление - ', round(x));

  writeln ('Целая часть - ', int(x));

  writeln ('Дробная часть - ', frac(x))

end.

2) Исследование целочисленных типов данных. Операции div и mod.

Трёхзначное число можно представить в виде следующей суммы: x = a·100 + b·10 + c, где а, b, с - цифры числа. Программа нахождения суммы цифр вводимого с клавиатуры целого трёхзначного числа.

program n_4;

  var x, a, b, c, s: integer;

begin

  writeln ('Нахождение суммы цифр трёхзначного числа');

  write ('Введите исходное число>>');

  readln (x);

  a:=x div 100;

  b:=x mod 100 div 10;

  c:=x mod 10;

  s:=a+b+c ;

  writeln ('s= ', s)

end.

3) Исследование порядковых типов данных. Порядковые типы характеризуются тем, что соответствующие им значения образуют конечное упорядоченное множество и каждое значение имеет свой порядковый номер. К порядковым типам относятся символьный, перечислимый и интервальный целые типы. Для выражений порядкового типа определены следующие функции:
1) ord(x) возвращает порядковый номер значения данного выражения. Для целых типов возвращает само значение x, для символьного – значение в диапазоне от 0 до 255, для перечислимого – значение в диапазоне от 0 до 65535. Для интервального типа результат зависит от свойств базового порядкового типа;
2) pred(x) возвращает значение, предшествующее значению данного выражения x;
3) succ(x) возвращает значение, следующее за значением данного выражения x; 

и процедуры:
   1) inc(x) присваивает переменной x следующее по порядку значение;
   2) dec(x) присваивает переменной x предшествующее значение.

program n_5;

  var a: char; kod: integer; b: string;

begin

  writeln ('Код и строка');

  write ('Введите исходную букву>>');

  readln (a);

  kod:=ord(a);

  b:=chr(kod–1)+a+chr(kod+1);

  writeln ('Код буквы ', a, '-', kod);

  writeln ('Строка: ', b)

end.

4) Исследование логического типа данных. Тип boolean (логический). Переменные и константы логического типа занимают 1 байт и принимают одно из двух значений, задаваемых предопределенными константами True (истина) и False (ложь). В логических выражениях можно использовать логические операции:
not (отрицание), and (логическое И), or (логическое ИЛИ), xor (логическое исключающее ИЛИ).

Пример 6.  Пусть ans - логическая переменная, n - целая переменная. В результате выполнения оператора присваивания ans:=n mod 2=0 переменной ans будет присвоено значение true при любом чётном n и false в противном случае.

program n_6;

  var n: integer; ans: boolean;

begin

  writeln ('Определение истинности высказывания о чётности числа');

  write ('Введите исходное число>>');

  readln (n);

  ans:=n mod 2=0;

  writeln ('Число ', n,' является четным - ', ans)

end.

program n_7;

  var a, b, c: integer; ans: boolean;

begin

  writeln ('Определение истинности высказывания о равнобедренном треугольнике');

  write ('Введите значения a, b, c>>');

  readln (a, b, c);

  ans:=(a=b) or (a=c) or (b=c);

  writeln ('Треугольник с длинами сторон ', a, ',', b,  ',', c, ' является равнобедренным - ', ans)

end.