Циклы
III. Повторение - последовательность действий, выполняемых многократно. Алгоритмы, содержащие конструкцию повторения, называют циклическими или циклами.
Последовательность действий, многократно повторяющаяся в процессе выполнения цикла, называется телом цикла.
В зависимости от способа организации повторений различают три типа циклов:
1) цикл с заданным условием продолжения работы;
2) цикл с заданным условием окончания работы;
3) цикл с заданным числом повторений.
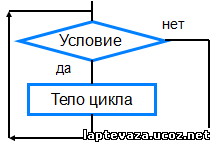
A) Цикл с заданным условием продолжения работы (цикл-ПОКА, цикл с предусловием). Логика работы этой конструкции описывается схемой, показанной на блок-схеме.
На алгоритмическом языке эта конструкция записывается так:
нц пока <условие>
<тело цикла (последовательность действий)>
кц
Выполняется цикл-ПОКА следующим образом:
1) проверяется условие (вычисляется значение логического выражения);
2) если условие удовлетворяется (Да), то выполняется тело цикла и снова осуществляется переход к проверке условия; если же условие не удовлетворяется, то выполнение цикла заканчивается. Возможны случаи, когда тело цикла не будет выполнено ни разу.
Пример 3. Требуется, не пользуясь операцией деления, получить частное q и остаток r от деления целого числа х на целое число у.
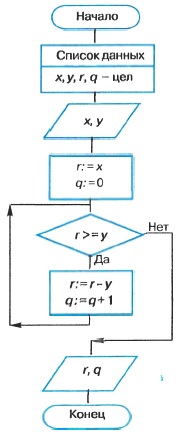
Представим операцию деления как последовательность вычитания делителя из делимого. Причём вычитать будем до тех пор, пока результат вычитания не станет меньше вычитаемого (делителя). В этом случае количество вычитаний будет частным от деления q, а последняя разность — остатком от деления r.
Исполним этот алгоритм для x=13 и y=5
|
Шаг алгоритма |
Операция |
Переменная |
Условие r >= y |
|||
|
x |
y |
r |
q |
|||
|
1 |
Ввод x |
13 |
- |
- |
- |
|
|
2 |
Ввод y |
13 |
5 |
- |
- |
|
|
3 |
r := x |
13 |
5 |
13 |
- |
|
|
4 |
q := 0 |
13 |
5 |
13 |
0 |
|
|
5 |
r >=y |
|
|
|
|
13>5, да |
|
6 |
r := r – y |
13 |
5 |
8 |
0 |
|
|
7 |
q := q +1 |
13 |
5 |
8 |
1 |
|
|
8 |
r >=y |
|
|
|
|
8>5, да |
|
9 |
r := r – y |
13 |
5 |
3 |
1 |
|
|
10 |
q := q +1 |
13 |
5 |
3 |
2 |
|
|
11 |
r >=y |
|
|
|
|
3>5, нет |
|
12 |
Вывод r |
|
|
3 |
|
|
|
13 |
Вывод q |
|
|
|
2 |
|
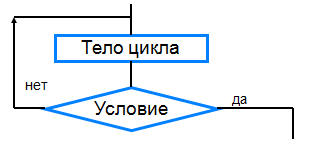 Б) Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием).
Б) Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием).
На алгоритмическом языке эта конструкция записывается так:
нц
<тело_цикла (последовательность действий)>
кц при <условие>
Выполняется цикл-ДО следующим образом:
1) выполняется тело цикла;
2) проверяется условие (вычисляется значение логического выражения); если условие не удовлетворяется (Нет), то снова выполняется тело цикла и осуществляется переход к проверке условия; если же условие удовлетворяется, то выполнение цикла заканчивается. В любом случае тело цикла будет выполнено хотя бы один раз.
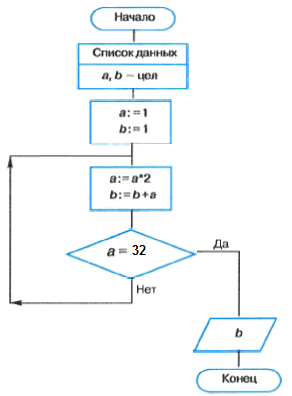
Пример 4. Вычислить переменную b по следующему алгоритму.
|
Шаг алгоритма |
Операция |
Переменная |
Условие |
|
|
a |
b |
a=32 |
||
|
1 |
a:=1 |
1 |
- |
|
|
2 |
b:=1 |
1 |
1 |
|
|
3 |
a:=a*2 |
2 |
1 |
|
|
4 |
b:=b+a |
2 |
3 |
|
|
5 |
a:=32 |
|
|
2=32 (нет) |
|
6 |
a:=a*2 |
4 |
3 |
|
|
7 |
b:=b+a |
4 |
7 |
|
|
8 |
a:=32 |
|
|
4=32 (нет) |
|
9 |
a:=a*2 |
8 |
7 |
|
|
10 |
b:=b+a |
8 |
15 |
|
|
11 |
a:=32 |
|
|
8=32 (нет) |
|
12 |
a:=a*2 |
16 |
15 |
|
|
13 |
b:=b+a |
16 |
31 |
|
|
17 |
a:=32 |
|
|
16=32 (нет) |
|
18 |
a:=a*2 |
32 |
15 |
|
|
19 |
b:=b+a |
32 |
47 |
|
|
20 |
a:=32 |
|
|
32=32 (да) |
|
21 |
Вывод b |
|
47 |
|
В) Цикл с заданным числом повторений (цикл-ДЛЯ, цикл с параметром).
На алгоритмическом языке эта конструкция записывается так:
нц для i от i1 до i2
<тело_цикла (последовательность действий)>
кц
В цикле-ДЛЯ всегда есть параметр цикла — величина целого типа, изменяющаяся в ходе выполнения цикла от своего начального значения до конечного значения.
Выполняется цикл-ДЛЯ следующим образом:
1) параметру цикла присваивается начальное значение;
2) параметр цикла сравнивается с конечным значением; если параметр цикла не превышает конечное значение, то выполняется тело цикла, увеличивается значение параметра цикла и снова осуществляется проверка параметра цикла; если же параметр цикла превышает конечное значение, то выполнение цикла заканчивается.
В отличие от двух предыдущих конструкций (цикл-ПОКА, цикл-ДО) цикл-ДЛЯ имеет строго фиксированное число повторений, что позволяет избежать зацикливания, т. е. ситуации, когда тело цикла выполняется бесконечно.
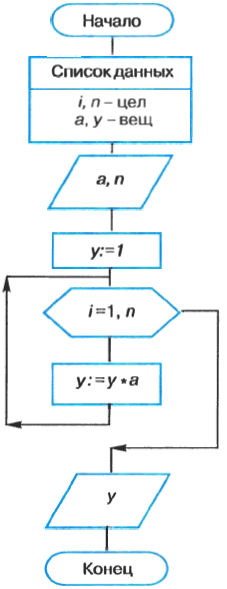 Пример 5. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа a.
Пример 5. Алгоритм вычисления степени с натуральным показателем n для любого вещественного числа a.
Исполним этот алгоритм для a=3 и n=2
|
Шаг алгоритма |
Операция |
Переменная |
Условие i <= n |
|||
|
a |
n |
y |
i |
|
||
|
1 |
Ввод a, n |
3 |
2 |
- |
- |
|
|
2 |
y := 1 |
3 |
2 |
1 |
- |
|
|
3 |
i := 1 |
3 |
2 |
1 |
1 |
|
|
4 |
i <= n |
|
|
|
|
1 <=2 (да) |
|
5 |
y := y * a |
3 |
2 |
3 |
1 |
|
|
6 |
i := i + 1 |
3 |
2 |
3 |
2 |
|
|
7 |
i <= n |
|
|
|
|
2 <=2 (да) |
|
8 |
y := y * a |
3 |
2 |
9 |
2 |
|
|
9 |
i := i + 1 |
3 |
2 |
9 |
3 |
|
|
10 |
i <= n |
|
|
|
|
3 <=2 (нет) |
|
11 |
Вывод y |
|
|
9 |
|
|




